空間内の3点を通る円
原点を $\textrm{O}(0,0,0)$ とする空間内の一直線上に並んでいない3点
\[
\textrm{P}_1(x_1, y_2, z_3), \ \textrm{P}_2(x_2, y_2, z_2), \ \textrm{P}_3(x_3, y_3, z_3)
\]
を通る円 $C$ の中心 $\textrm{C}(c_1, c_2, c_3)$ と半径 $r$,円弧のパラメータ表示を求める.
計算の方針と概略
\[
\rm{P}_1(2,3,2), \ \rm{P}_2(5,0,5), \ \rm{P}_3(4,-5,0)
\]
を通る円の中心の座標 $\textrm{C}(c_1, c_2, c_3)$ と半径 $r$,円周上の点のパラメータ表示を求める.
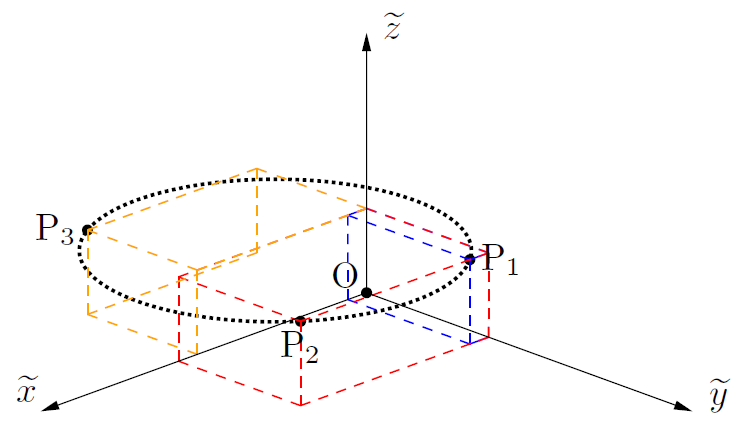
【3点の配置と求める円の参考図】
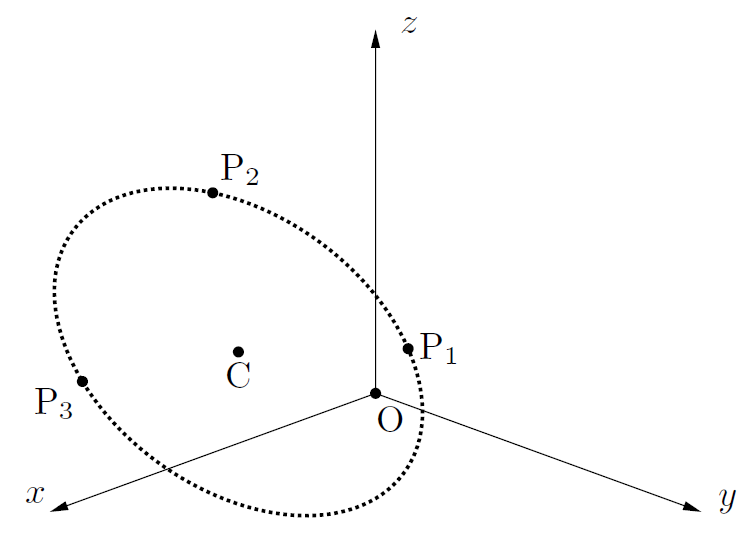
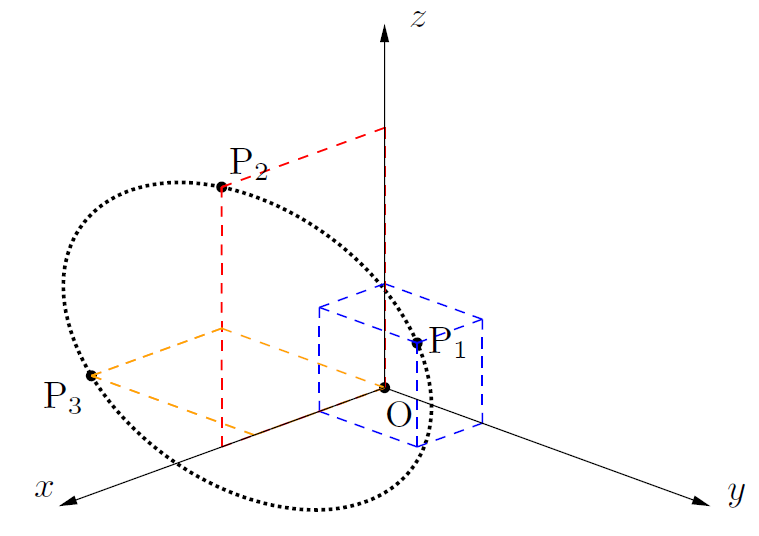
【Y軸の正の方向から見た図】
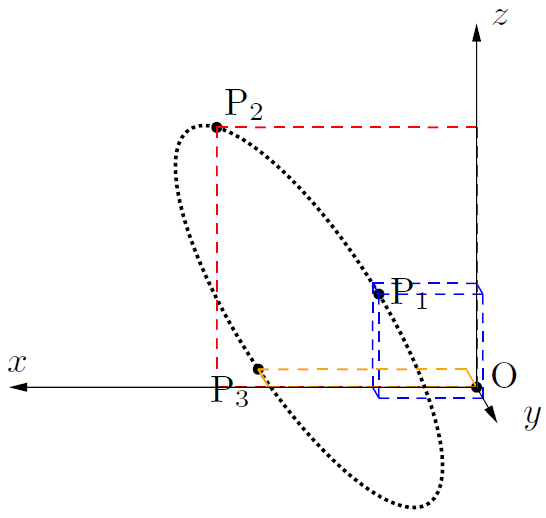
方針 1:ベクトル・平面の方程式を使って求める
円の中心の座標と半径
- $\textrm{P}_1$ からの距離と $\textrm{P}_2$ からの距離とが等しくなるような平面 $\alpha_1$ を求める
- $\textrm{P}_1$ からの距離と $\textrm{P}_3$ からの距離とが等しくなるような平面 $\alpha_2$ を求める
- 3点 $\textrm{P}_1, \ \textrm{P}_2, \ \textrm{P}_3$ を通る平面 $\beta$ を求める
- 円 $C$ の中心の座標を3つの平面 $\alpha_1, \ \alpha_2, \ \beta$ の交点として求める
- 円の半径を計算する
パラメータ表示
- 円 $C$ の円周上の点を $\textrm{X}(x,y,z)$ とおくと次が成り立つ:
\[
\overrightarrow{\textrm{OX}} = \overrightarrow{\textrm{OC}} + \overrightarrow{\textrm{CX}}
\]
- 3点 $\textrm{P}_1, \ \textrm{P}_2, \ \textrm{P}_3$ を通る平面 $\beta$ 上で以下を満たす点 $\textrm{U}, \ \textrm{V}$ を考える:
\[
\begin{align*}
1. \qquad & \overrightarrow{\textrm{P}_1\textrm{U}} \cdot \overrightarrow{\textrm{P}_1\textrm{V}} = 0 \\
2. \qquad & |\overrightarrow{\textrm{P}_1\textrm{U}}| = |\overrightarrow{\textrm{P}_1\textrm{V}}| = 1
\end{align*}
\]
- このとき円周のパラメータ表示は,パラメータ $\theta$ を用いて以下のように表せる:
\[
\overrightarrow{\text{OX}} = \overrightarrow{\textrm{OC}} + (r\cos{\theta}) \ \overrightarrow{\textrm{P}_1\textrm{U}} + (r\sin{\theta}) \ \overrightarrow{\textrm{P}_1\textrm{V}}
\]
方針 2:行列を使って求める
線形代数を使って座標系を回転(基底の変換)させて求める.
- 座標系を回転させて,3点のある成分が等しくなるような新しい座標系を求める
- 新しい座標系上で,3点を通る円を2つの成分の計算だけで求める
- 座標系を元に戻して,元の(標準の)座標系での円の表現を求める
方針 1:ベクトル・平面の方程式を使って求める
$\textrm{P}_1$ からの距離と $\textrm{P}_2$ からの距離とが等しくなるような平面 $\alpha_1$ を求める
【平面 $\alpha_1$ の参考図】
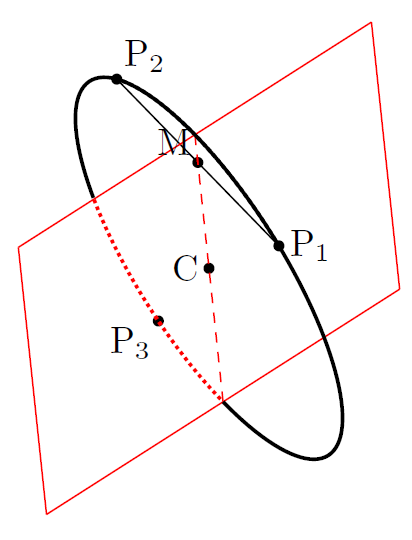
2点間の距離の公式を用いる
詳細(click)
平面 $\alpha_1$ 上の点を $\textrm{Q}(x, y, z)$ とおく.$\textrm{P}_1\textrm{Q}$ の長さの2乗を計算すると
\[
\begin{align*}
\textrm{P}_1\textrm{Q}^2
&= (x-2)^2 + (y-3)^2 + (z-2)^2 \\
&= x^2 + y^2 + z^2-4x-6y-4z + 17
\end{align*}
\]
$\textrm{P}_2\textrm{Q}$ の長さの2乗を計算すると
\[
\begin{align*}
\textrm{P}_2\textrm{Q}^2
&= (x-5)^2 + (y-0)^2 + (z-5)^2 \\
&= x^2 + y^2 + z^2-10x-10z+50
\end{align*}
\]
これが等しいから,$\textrm{P}_1\textrm{Q}^2 = \textrm{P}_2\textrm{Q}^2$ として整理すると
\[
2x-2y + 2z = 11
\]
を得る.これが平面 $\alpha_1$ の式である.
ベクトルに直交する平面を求める公式を用いる
詳細(click)
あるベクトルに直交する平面の方程式は以下の公式で求めることができる:
\[
a(x-x_0)+b(y-y_0)+c(z-z_0) = 0
\]
で与えられる.
証明(click)
求める平面上の点を $\textrm{X}(x,y,z)$ とおく.いま $\overrightarrow{\textrm{X}\textrm{X}_0}$ と $\overrightarrow{a}$ は直交するから内積は $0$ である.すなわち
\[
\overrightarrow{a} \cdot \overrightarrow{\textrm{X}\textrm{X}_0} = 0
\]
が成り立つ.これを展開すれば求める式を得る.
$\overrightarrow{\textrm{P}_1 \textrm{P}_2} = \overrightarrow{\textrm{O} \textrm{P}_2}-\overrightarrow{\textrm{O} \textrm{P}_1} = (3, -3, 3)$ である.
また,点 $\textrm{P}_1$ と点 $\textrm{P}_2$ の中点を $\textrm{M}$ とおくと $\displaystyle \textrm{M}\left(\frac{7}{2},\frac{3}{2},\frac{7}{2}\right)$ である.
いま 平面 $\alpha_1$ はベクトル $\overrightarrow{\textrm{P}_1\textrm{P}_2}$ と直交して,かつ点 $\textrm{M}$ を通るから,その方程式は
\[
3\left(x-\frac{7}{2}\right)-3\left(x-\frac{3}{2}\right) + 3\left(x-\frac{3}{2}\right) = 0
\]
これを整理して
\[
2x-2y + 2z = 11
\]
が平面 $\alpha_1$ の方程式である.
$\textrm{P}_1$ からの距離と $\textrm{P}_3$ からの距離とが等しくなるような平面 $\alpha_2$ を求める
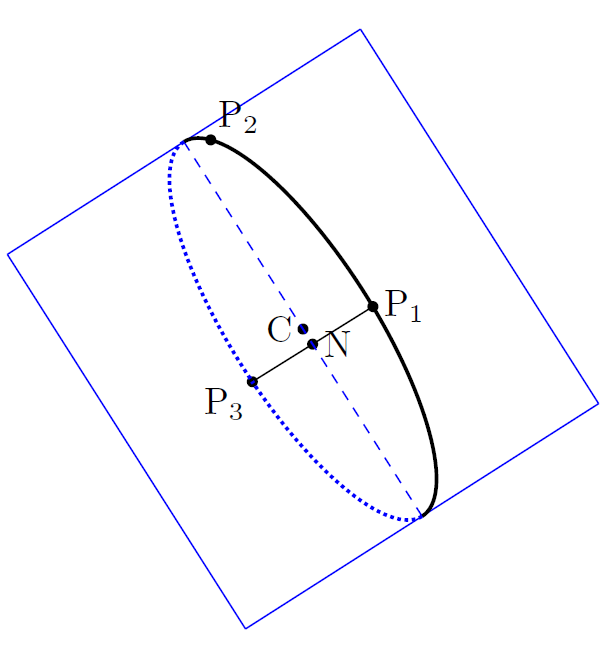
2点間の距離の公式を用いる
詳細(click)
平面 $\alpha_2$ 上の点を $\textrm{Q}(x, y, z)$ とおく.$\textrm{P}_1\textrm{Q}$ の長さの2乗を計算すると
\[
\begin{align*}
\textrm{P}_1\textrm{Q}^2
&= (x-2)^2 + (y-3)^2 + (z-2)^2 \\
&= x^2 + y^2 + z^2-4x-6y-4z + 17
\end{align*}
\]
$\textrm{P}_3\textrm{Q}$ の長さの2乗を計算すると
\[
\begin{align*}
\textrm{P}_3\textrm{Q}^2
&= (x-4)^2 + (y+5)^2 + (z-0)^2 \\
&= x^2 + y^2 + z^2-8x+10y+41
\end{align*}
\]
これが等しいから,$\textrm{P}_1\textrm{Q}^2 = \textrm{P}_3\textrm{Q}^2$ として整理すると
\[
x-4y-z=6
\]
を得る.これが平面 $\alpha_2$ の式である.
ベクトルに直交する平面を求める公式を用いる
証明(click)
$\overrightarrow{\textrm{P}_1 \textrm{P}_3} = \overrightarrow{\textrm{O} \textrm{P}_3}-\overrightarrow{\textrm{O} \textrm{P}_1} = (2, -8, -2)$ である.
また,点 $\textrm{P}_1$ と点 $\textrm{P}_3$ の中点を $\textrm{N}$ とおくと $\textrm{N}(3, -1, 1)$ である.
いま 平面 $\alpha_2$ はベクトル $\overrightarrow{\textrm{P}_1\textrm{P}_3}$ と直交して,かつ点 $\textrm{N}$ を通るから,その方程式は
\[
2(x-3)-8(y+1)-2(z-1) = 0
\]
これを整理して
\[
x-4y-z=6
\]
が平面 $\alpha_2$ の方程式である.
3点 $\textrm{P}_1$,$\textrm{P}_2$,$\textrm{P}_3$ を通る平面 $\beta$ を求める
平面の方程式 $ax+by+cz=d$ から連立方程式を立てて求める
詳細(click)
平面 $\beta$ の方程式を $ax + by + cz = d$ とおく.
3点 $\textrm{P}_1, \ \textrm{P}_2, \ \textrm{P}_3$ の座標をそれぞれ代入すると
\[
\begin{cases}
2a+3b+2c=d & \cdots\cdots (1)\\
5a+0b+5c=d & \cdots\cdots (2)\\
4a-5b+0c=d & \cdots\cdots (3)
\end{cases}
\]
が成り立つ.$a, b, c$ をそれぞれ $d$ の式で表す.$(2)$ と $(3)$ をそれぞれ整理すると
\[
c = -a+\frac{1}{5}d, \quad b = \frac{4}{5}a-\frac{1}{5}d
\]
を得る.これを $(1)$ に代入すると
\[
d = 2a+3b+2c = \frac{12}{5}a-\frac{1}{5}d
\]
であるから,$d$ を移行して $a$ について整理すれば
\[
a = \frac{1}{2}d
\]
を得る.$b$,$c$ の式に代入しなおして
\[
b = \frac{1}{5}d, \quad c = -\frac{3}{10}d
\]
が得られた.これを平面の方程式 $ax+by+cz=d$ に代入して整理すれば,
\[
5x+2y-3z=10
\]
が平面 $\beta$ の方程式である.
※ $d=0$ では式が意味を持たなくなるので,$d \neq 0$ と考えて $d$ を消去した.
ベクトルを使って求める
詳細(click)
$\textrm{Q}$ を平面 $\beta$ 上の点とすると,実数 $s,\ t$ を用いて
\[
\overrightarrow{\textrm{P}_1\textrm{Q}} = s \ \overrightarrow{\textrm{P}_1\textrm{P}_2} + t \ \overrightarrow{\textrm{P}_1\textrm{P}_3}
\]
と表すことができる.$\textrm{Q}(x,y,z)$ とおくと上式は
\[
\begin{align*}
(x-2, y-3, z-2)
&=(3s, -3s, 3s)+(2t, -8t, -2t)\\
&=(3s+2t, -3s-8t, 3s-2t)
\end{align*}
\]
と展開できる.各成分を比較して
\[
\begin{cases}
x=+3s+2t+2 & \cdots\cdots (4)\\
y=-3s-8t+3 & \cdots\cdots (5)\\
z=+3s-2t+2 & \cdots\cdots (6)
\end{cases}
\]
が得られる.ここから $s, \ t$ を消去して $x, \ y, \ z$ の関係式を求める.$(4)-(6)$,$(4)+(5)$ をそれぞれ計算すると $s$ が消去できて
\[
x-z=4t, \quad x+y=-6t+5
\]
となるから,$t$ を消去して整理すれば
\[
5x+2y-3z=10
\]
が平面 $\beta$ の方程式である.
円 $C$ の中心の座標を3つの平面 $\alpha_1, \ \alpha_2, \ \beta$ の交点として求める
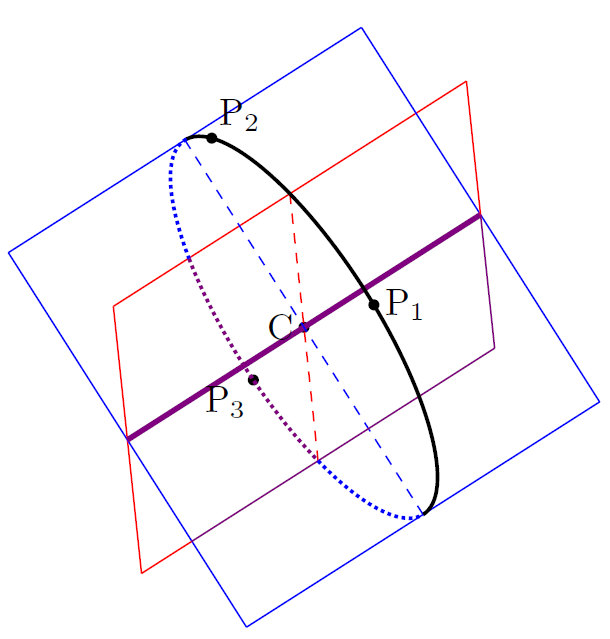
平面の方程式を連立して求める
詳細(click)
円の中心 $\textrm{C}$ は平面 $\alpha_1, \ \alpha_2, \ \beta$ の交点であるから,得られた3つの方程式を連立すれば座標が得られる.
\[
\begin{cases}
2x-2y+2z=11 & \cdots\cdots (\alpha_1)\\
\ \ x-4y-\ \ z=\ \ 6 & \cdots\cdots (\alpha_2)\\
5x+2y-3z=10 & \cdots\cdots (\beta)
\end{cases}
\]
$(\alpha_1)+(\beta)$,$(\alpha_2)-2\times(\beta)$ をそれぞれ計算して
\[
7x-z=21, \quad -3x-5z=-16
\]
を得る.$z=7x-21$ を2つ目の式に代入して $z$ を消去すれば
\[
x = \frac{121}{38}
\]
および
\[
z=7x-21=\frac{49}{38}
\]
を得る.$(\alpha_1)$ から $y$ を求めれば
\[
y=x+z-\frac{11}{2}=-\frac{39}{38}
\]
であるから,円の中心 $\textrm{C}$ の座標は
\[
\left(\frac{121}{38}, -\frac{39}{38}, \frac{49}{38}\right)
\]
である.
共有点が満たす条件をパラメータで表現して求める
詳細(click)
円の中心 $\textrm{C}$ は平面 $\alpha_1, \ \alpha_2, \ \beta$ の交点であるから,$\textrm{C}(x,y,z)$ とおくと
\[
\begin{cases}
2x-2y+2z-11=0 & \cdots\cdots (\alpha_1)\\
\ \ x-4y-\ \ z-\ \ 6=0 & \cdots\cdots (\alpha_2)\\
5x+2y-3z-10=0 & \cdots\cdots (\beta)
\end{cases}
\]
が同時に成り立つ.したがって実数 $k, \ \ell$ を用いて
\[
(2x-2y+2z-11) + k(x-4y-z-6) + \ell(5x+2y-3z-10) = 0
\]
という式を考えると,この式は各 $( \ )$ が全て $0$ になるから,$k, \ \ell$ がどのような値であってもつねに成り立つ.上式を $x, y, z$ で整理しなおすと
\[
x(2+2k+5\ell)+y(-2-4k+2\ell)+z(2-k-3\ell)+(-11-6k-10\ell)=0 \tag{$\heartsuit$}
\]
となる.まずは $x$ を求めるために $y$ と $z$ を消去するような $k, \ \ell$ を求める.それぞれの係数が $0$ になればよいから,連立方程式
\[
\begin{cases}
-2-4k+2\ell=0 & \\
+2-5k-3\ell=0 &
\end{cases}
\]
を解いて
\[
k = -\frac{1}{7}, \quad \ell = \frac{5}{7}
\]
とすればよい.これを $(\heartsuit)$ に代入して
\[
x = \frac{121}{38}
\]
を得る.$y$ を求めるためには $x$ と $z$ の係数が $0$ になるような $k, \ \ell$ を求めればよい.
\[
\begin{cases}
2+k+5\ell=0 & \\
2-k-3\ell=0 &
\end{cases}
\]
から
\[
k=8, \quad \ell =-2
\]
が得られるので,これを $(\heartsuit)$ に代入すれば
\[
y =-\frac{39}{38}
\]
を得る.$z$ も同様にして $x$ と $y$ の係数を消去するような $k, \ \ell$ を求めればよいから
\[
\begin{cases}
+2+ \ \ k+5\ell=0 & \\
-2-4k+2\ell=0 &
\end{cases}
\]
より
\[
k=-\frac{7}{11}, \quad \ell = -\frac{3}{11}
\]
であって,これを $(\heartsuit)$ に代入すれば
\[
z = \frac{49}{38}
\]
を得られる.したがって円の中心 $\textrm{C}$ の座標は
\[
\left(\frac{121}{38}, -\frac{39}{38}, \frac{49}{38}\right)
\]
である.
円の半径を計算する
2点間の距離の公式で求める
詳細(click)
半径を $r$ とすると
\[
r = \textrm{P}_1\textrm{C} = \textrm{P}_2\textrm{C} = \textrm{P}_3\textrm{C}
\]
が成り立つから,$r$ は例えば $\textrm{P}_1$ と $C$ の距離として求めることができる.
\[
\begin{align*}
\textrm{P}_1\textrm{C}^2
&= \left(2-\frac{121}{38}\right)^2 + \left(3+\frac{39}{38}\right)^2 + \left(2-\frac{49}{38}\right)^2 \\
&= \frac{1}{38^2}\Bigl((76-121)^2+(114+39)^2+(76-49)^2\Bigr) \\
&= \frac{1}{38^2}\bigl(45^2+153^2+27^2\bigr) \\
&= \frac{9^2}{38^2}\bigl(5^2+17^2+3^2\bigr) \\
&= \frac{9^2 \cdot 323}{38^2} \\
&= \frac{9^2 \cdot 17}{2^2 \cdot 19}
\end{align*}
\]
である.$r = \textrm{P}_1\textrm{C} > 0$ であるから
\[
r = \sqrt{\frac{9^2 \cdot 17}{2^2 \cdot 19}} = \frac{9\sqrt{17}}{2\sqrt{19}}
\]
が得られた.
図形と計量の知識を使って求める
詳細(click)
正弦定理を用いて,外接円の半径として求める.$\triangle \textrm{P}_1 \textrm{P}_2 \textrm{P}_3$ の各辺の長さは
\[
\textrm{P}_1\textrm{P}_2 = 3\sqrt{3}, \quad \textrm{P}_1\textrm{P}_3 = 6\sqrt{2}, \quad \textrm{P}_2\textrm{P}_3 = \sqrt{51}
\]
であるから,余弦定理より
\[
\cos{\textrm{P}_1} = \frac{(3\sqrt{3})^2 + (6\sqrt{2})^2 + (\sqrt{51})^2}{2 \cdot 3\sqrt{3} \cdot 6\sqrt{2}} = \frac{2\sqrt{6}}{9}
\]
$\sin{\textrm{P}_1} > 0$ に注意して,三角比の相互関係より
\[
\sin{\textrm{P}_1} = \sqrt{1-\left(\frac{2\sqrt{6}}{9}\right)^2} = \frac{\sqrt{57}}{9}
\]
を得る.正弦定理より
\[
r = \frac{\textrm{P}_2\textrm{P}_3}{2 \sin{\textrm{P}_1}} = \frac{9\sqrt{51}}{2 \sqrt{57}} = \frac{9 \sqrt{17}}{2 \sqrt{19}}
\]
が得られた.
円周のパラメータ表示を求める
円 $C$ の円周上の点を $\textrm{X}(x,y,z)$ とおくと次が成り立つ:
\[
\overrightarrow{\textrm{OX}} = \overrightarrow{\textrm{OC}} + \overrightarrow{\textrm{CX}}
\]
3点 $\textrm{P}_1, \ \textrm{P}_2, \ \textrm{P}_3$ を通る平面 $\beta$ 上で以下を満たす点 $\textrm{U}, \ \textrm{V}$ を考える.
点 $\textrm{U}$ は $\overrightarrow{\textrm{P}_1\textrm{U}}$ と $\overrightarrow{\textrm{P}_1\textrm{P}_2}$ が平行になるようにとることにすると,$|\overrightarrow{\textrm{P}_1\textrm{P}_2}| = 3\sqrt{3}$ であるから
\[
\overrightarrow{\textrm{P}_1\textrm{U}} = \left(\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)
\]
となる.この点 $\textrm{U}$ を基準に点 $\textrm{V}$ を求める.
ベクトルを用いて求める
詳細(click)
点 $\textrm{V}$ は平面 $\beta$ 上にあるから,実数 $s, \ t$ を用いて
\[
\overrightarrow{\textrm{P}_1\textrm{V}} = s \ \overrightarrow{\textrm{P}_1\textrm{P}_2} + t \ \overrightarrow{\textrm{P}_1\textrm{P}_3}
\]
と表すことができる.$\overrightarrow{\textrm{P}_1\textrm{V}}$ と $\overrightarrow{\textrm{P}_1\textrm{P}_2}$ は直交するから内積が $0$ になるので
\[
\begin{align*}
0
&= \overrightarrow{\textrm{P}_1\textrm{P}_2} \cdot \overrightarrow{\textrm{P}_1\textrm{V}} \\
&= s \ |\overrightarrow{\textrm{P}_1\textrm{P}_2}|^2 + t \ \overrightarrow{\textrm{P}_1\textrm{P}_2} \cdot \overrightarrow{\textrm{P}_1\textrm{P}_3} \\
&= 27s + 24t
\end{align*}
\]
より
\[
s = -\frac{8}{9}t
\]
が成り立つ.これを用いて $\overrightarrow{\textrm{P}_1\textrm{V}}$ の成分表示から $s$ を消去すると
\[
\begin{align*}
\overrightarrow{\textrm{P}_1\textrm{V}}
&= -\frac{8}{9}t \ \overrightarrow{\textrm{P}_1\textrm{P}_2} + t \ \overrightarrow{\textrm{P}_1\textrm{P}_3} \\
&= \left(-\frac{2}{3}t, -\frac{16}{3}t, -\frac{14}{3}t \right)
\end{align*}
\]
$|\overrightarrow{\textrm{P}_1\textrm{V}}|=1$ であるから
\[
1 = \left(-\frac{2}{3}t\right)^2 + \left(-\frac{16}{3}t\right)^2 + \left(-\frac{14}{3}t\right)^2 = \frac{152}{3}t^2
\]
が成り立つ.$t$ は $+$ と $-$ が考えられるが,今回は $+$ を採用して
\[
t = \frac{3}{2\sqrt{114}}
\]
とすれば
\[
\overrightarrow{\textrm{P}_1\textrm{V}}
= \left(\frac{1}{\sqrt{114}}, \frac{8}{{\sqrt{114}}}, \frac{7}{{\sqrt{114}}} \right)
\]
が得られる.
平面の方程式を利用して求める
詳細(click)
$\overrightarrow{\textrm{P}_1\textrm{V}} = (a, b, c)$ とおくと,点 $\textrm{V}$ の座標は
\[
\overrightarrow{\textrm{O}\textrm{V}} = \overrightarrow{\textrm{O}\textrm{P}_1} + \overrightarrow{\textrm{P}_1\textrm{V}} = (a+2, b+3, c+2)
\]
と表示できる.この点は平面 $\beta$ 上にあるから $5x+2y-3z=10$ を満たすので
\[
5(a+2)+2(b+3)-3(c+2)=10
\]
より
\[
5a+2b-3c = 0
\]
が成り立つ.また $\overrightarrow{\textrm{P}_1\textrm{V}}$ と $\overrightarrow{\textrm{P}_1\textrm{P}_2}$ は直交するから内積が $0$ になるので
\[
0 = \overrightarrow{\textrm{P}_1\textrm{P}_2} \cdot \overrightarrow{\textrm{P}_1\textrm{V}} = 3a-3b+3c
\]
より
\[
a-b+c = 0
\]
が成り立つ.これらの式から $b$,$c$ を消去して $a$ の式で表すと
\[
b = 8a, \quad c = 7a
\]
となるから
\[
\overrightarrow{\textrm{P}_1\textrm{V}} = (a, 8a, 7a)
\]
を得る.$|\overrightarrow{\textrm{P}_1\textrm{V}}|=1$ であるから
\[
1 = a^2 + 64a^2 + 49a^2 = 114a^2
\]
が成り立つ.$a$ は $+$ と $-$ が考えられるが,今回は $+$ を採用して
\[
a = \frac{1}{\sqrt{114}}
\]
とすれば
\[
\overrightarrow{\textrm{P}_1\textrm{V}}
= \left(\frac{1}{\sqrt{114}}, \frac{8}{{\sqrt{114}}}, \frac{7}{{\sqrt{114}}} \right)
\]
が得られる.
$\textrm{C}, \ \textrm{X}, \ \textrm{P}_1, \ \textrm{U}, \ \textrm{V}$ はすべて平面 $\beta$ 上にあるから,$\overrightarrow{\textrm{CX}}$ は実数 $m, n$ を用いて次のように表せる:
\[
\overrightarrow{\textrm{CX}} = m \ \overrightarrow{\textrm{P}_1\textrm{U}} + n \ \overrightarrow{\textrm{P}_1\textrm{V}}
\]
ここで $\textrm{C}$ は円の中心であるから,半径 $r$ と実数 $m, n$ は
\[
r^2 = |\overrightarrow{\textrm{CX}}|^2 = m^2 |\overrightarrow{\textrm{P}_1\textrm{U}}|^2 + 2mn \ \overrightarrow{\textrm{P}_1\textrm{U}} \cdot \overrightarrow{\textrm{P}_1\textrm{V}} + n^2 |\overrightarrow{\textrm{P}_1\textrm{V}}|^2 = m^2 + n^2
\]
を満たす.このとき $m, n$ は半径 $r$ とパラメータ $\theta$ を用いて次のように表せる:
\[
m = r\cos{\theta}, \quad n = r\sin{\theta}
\]
したがって,円周のパラメータ表示は,パラメータ $\theta$ を用いて
\[
\overrightarrow{\text{OX}}
= \overrightarrow{\textrm{OC}} + (r\cos{\theta}) \ \overrightarrow{\textrm{P}_1\textrm{U}} + (r\sin{\theta}) \ \overrightarrow{\textrm{P}_1\textrm{V}}
\]
と表せる.各成分を書き下すと
\[
\begin{cases}
\displaystyle x=\frac{121}{38}+\frac{9\sqrt{17}}{38\sqrt{6}}\Bigl(\sqrt{38}\cos{\theta}+\sin{\theta}\Bigr) & \\
\displaystyle y=-\frac{39}{38}-\frac{9\sqrt{17}}{38\sqrt{6}}\Bigl(\sqrt{38}\cos{\theta}-8\sin{\theta}\Bigr) & \\
\displaystyle z=\frac{49}{38}+\frac{9\sqrt{17}}{38\sqrt{6}}\Bigl(\sqrt{38}\cos{\theta}+7\sin{\theta}\Bigr) & \\
\end{cases}
\]
となる.
方針 2:線形代数を使って求める
記号のルール
詳細(click)
- 行列 $A$,ベクトル $\boldsymbol{a}$ の転置を ${}^{\textsf{t}} A$,${}^{\textsf{t}} \boldsymbol{a}$ で表す
- $\boldsymbol{a}$ と $\boldsymbol{b}$ の内積を $\boldsymbol{a} \cdot \boldsymbol{b}$ で表す.すなわち
\[
\boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{a}{}^{\textsf{t}} \boldsymbol{b}
\]
- $\boldsymbol{a}$ の大きさを $\| \boldsymbol{a} \|$ で表す.すなわち
\[
\| \boldsymbol{a} \| = \sqrt{\boldsymbol{a} \cdot \boldsymbol{a}} = \sqrt{\boldsymbol{a}{}^{\textsf{t}} \boldsymbol{a}}
\]
- $\boldsymbol{a}$ と $\boldsymbol{b}$ の外積(クロス積)を $\boldsymbol{a} \times \boldsymbol{b}$ で表す
新しい座標系を求める
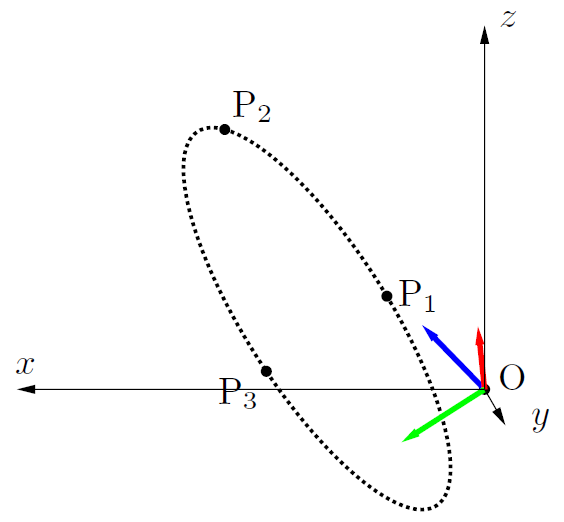
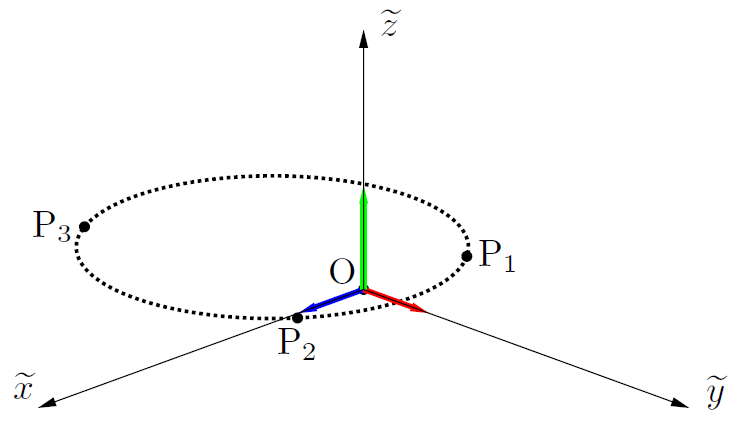
詳細(click)
$\textrm{P}_1, \ \textrm{P}_2, \ \textrm{P}_3$ を表す位置ベクトルをそれぞれ $\boldsymbol{p}_1, \ \boldsymbol{p}_2, \ \boldsymbol{p}_3$ とする.
$\boldsymbol{g}_1, \ \boldsymbol{g}_2$ をそれぞれ $\textrm{P}_1$ から $\textrm{P}_2$,$\textrm{P}_1$ から $\textrm{P}_3$ へのベクトルとする:
\[
\boldsymbol{g}_1 = \boldsymbol{p}_2-\boldsymbol{p}_1 =\left[
\begin{array}{c}
3 \\
-3 \\
3 \\
\end{array}
\right], \quad \|\boldsymbol{g}_1\| = 3\sqrt{3}
\]
\[
\boldsymbol{g}_2 = \boldsymbol{p}_3-\boldsymbol{p}_1 =
\left[
\begin{array}{c}
2 \\
-8 \\
-2 \\
\end{array}
\right], \quad \|\boldsymbol{g}_2\| = 6\sqrt{2}
\]
新しい座標系の $\widetilde{x}, \ \widetilde{y}, \ \widetilde{z}$ 方向を表す正規直交基底を $\widetilde{\boldsymbol{e}}_1, \ \widetilde{\boldsymbol{e}}_2, \ \widetilde{\boldsymbol{e}}_3$ とする.$\widetilde{\boldsymbol{e}}_1$ は $\boldsymbol{g}_1$ の方向にとる:
\[
\widetilde{\boldsymbol{e}}_1 = \frac{\boldsymbol{g}_1}{\|\boldsymbol{g}_1\|} = \frac{1}{\sqrt{3}}
\left[
\begin{array}{c}
1 \\
-1 \\
1 \\
\end{array}
\right]
\]
今回は円 $C$ が新しい座標系で $\widetilde{x}\widetilde{y}$ 平面上に乗るようにしたい.したがって $\widetilde{\boldsymbol{e}}_3$ は $\boldsymbol{g}_1$ と $\boldsymbol{g}_2$ に直交する方向,すなわちこれらの外積の方向にとる:
\[
\boldsymbol{g}_1 \times \boldsymbol{g}_2 =
\left[
\begin{array}{c}
6+24 \\
6+6 \\
-24+6 \\
\end{array}
\right] =
\left[
\begin{array}{c}
30 \\
12 \\
-18 \\
\end{array}
\right]
\]
\[
\|\boldsymbol{g}_1 \times \boldsymbol{g}_2\| = 6\sqrt{38}
\]
\[
\widetilde{\boldsymbol{e}}_3 = \frac{\boldsymbol{g}_1\times \boldsymbol{g}_2}{\|\boldsymbol{g}_1 \times \boldsymbol{g}_2\|} = \frac{1}{\sqrt{38}}
\left[
\begin{array}{c}
5\\
2 \\
-3 \\
\end{array}
\right]
\]
$\widetilde{\boldsymbol{e}}_2$ は $\widetilde{\boldsymbol{e}}_1$ と $\widetilde{\boldsymbol{e}}_3$ に直交する方向にとる必要があるから,再び外積を考えて
\[
\begin{align*}
\widetilde{\boldsymbol{e}}_2
= \widetilde{\boldsymbol{e}}_3 \times \widetilde{\boldsymbol{e}}_1
=
\frac{1}{\sqrt{114}}
\left[
\begin{array}{c}
1\\
8\\
7\\
\end{array}
\right]
\end{align*}
\]
とすれば
\[
A = [\widetilde{\boldsymbol{e}}_1 \ \widetilde{\boldsymbol{e}}_2 \ \widetilde{\boldsymbol{e}}_3] =
\frac{1}{\sqrt{114}}
\left[
\begin{array}{rrr}
\sqrt{38} & 1 & 5\sqrt{3} \\
-\sqrt{38} & 8 & 2\sqrt{3} \\
\sqrt{38} & 7 & -3\sqrt{3}
\end{array}
\right]
\]
は新しい座標系の基底を並べた直交行列であり
\[
A^{-1} = {}^{\textsf{t}} A
\]
を満たす.
新しい座標系上で円の方程式とパラメータ表示を求める
詳細(click)
新しい座標系における $\rm{P}_1, \ \rm{P}_2, \ \rm{P}_3$ の位置ベクトルを $\widetilde{\boldsymbol{p}}_1, \ \widetilde{\boldsymbol{p}}_2, \ \widetilde{\boldsymbol{p}}_3$ とすると
\[
\widetilde{\boldsymbol{p}}_1 = {}^{\textsf{t}} A\boldsymbol{p}_1 = \frac{1}{\sqrt{114}}
\left[
\begin{array}{c}
\sqrt{38} \\
40 \\
10\sqrt{3} \\
\end{array}
\right]
\]
\[
\widetilde{\boldsymbol{p}}_2 = {}^{\textsf{t}} A\boldsymbol{p}_2 = \frac{1}{\sqrt{114}}
\left[
\begin{array}{c}
10\sqrt{38} \\
40 \\
10\sqrt{3} \\
\end{array}
\right]
\]
\[
\widetilde{\boldsymbol{p}}_3 = {}^{\textsf{t}} A\boldsymbol{p}_3 = \frac{1}{\sqrt{114}}
\left[
\begin{array}{c}
9\sqrt{38} \\
-36 \\
10\sqrt{3} \\
\end{array}
\right]
\]
が成り立つ.3点の新しい $\widetilde{z}$ 座標は意図したとおりに一致していて,3点は平面
\[
\widetilde{z} = \frac{10\sqrt{3}}{\sqrt{114}} = \frac{10}{\sqrt{38}}
\]
の上に存在することが判る.3点を通る円の中心は
\[
\left(\widetilde{c}_1, \widetilde{c}_2, \frac{10}{\sqrt{38}}\right)
\]
と表せるから,半径を $r$ とすれば,3点を通る円の方程式は
\[
(\widetilde{x}-\widetilde{c}_1)^2 + (\widetilde{y}-\widetilde{c}_2)^2 = r^2, \quad \widetilde{z} = \frac{10}{\sqrt{38}}
\]
となる.この方程式を満たす $\widetilde{c}_1, \widetilde{c}_2, r$ を求めればよい.$\widetilde{z}$ 座標を考慮しなくてよいから,これは $xy$ 平面上の円の方程式を求めるときと同じ要領でできる.
求める円の方程式を
\[
\widetilde{x}^2 + \widetilde{y}^2 + \ell \widetilde{x} + m \widetilde{y} + n = 0
\]
とおく.3点の $(\widetilde{x}, \widetilde{y})$ 座標の値を代入して
\[
\begin{cases}
\displaystyle \frac{1}{3} + \frac{800}{57}+\frac{1}{\sqrt{3}}\ell + \frac{40}{\sqrt{114}}m + n = 0 & \cdots \cdots (1)\\
\displaystyle \frac{100}{3} + \frac{800}{57} + \frac{10}{\sqrt{3}}\ell + \frac{40}{\sqrt{114}}m + n = 0 & \cdots \cdots (2)\\
\displaystyle 27 + \frac{216}{19} + \frac{9}{\sqrt{3}}\ell-\frac{36}{\sqrt{114}}m + n = 0 & \cdots \cdots (3)
\end{cases}
\]
なる連立方程式を解く.$(2)-(1)$ の差から
\[
33+\frac{9}{\sqrt{3}}\ell = 0
\]
すなわち
\[
\ell = -\frac{11}{\sqrt{3}}
\]
を得る.$(1)$, $(3)$ に代入して整理すると
\[
\begin{cases}
\displaystyle \frac{610}{57}+\frac{40}{\sqrt{114}} m + n = 0 \\
\displaystyle \frac{102}{19}-\frac{36}{\sqrt{114}}m + n = 0
\end{cases}
\]
を得る.これを解いて
\[
m = -\frac{8}{\sqrt{114}}, \quad n = -\frac{150}{19}
\]
となるから,求める方程式は
\[
\widetilde{x}^2 + \widetilde{y}^2-\frac{11}{\sqrt{3}}\widetilde{x}-\frac{8}{\sqrt{114}}\widetilde{y}-\frac{150}{19} = 0
\]
である.$\widetilde{x}, \widetilde{y}$ をそれぞれ平方完成すれば
\[
\left(\widetilde{x}-\frac{11}{2\sqrt{3}}\right)^2-\frac{121}{12} + \left(\widetilde{y}-\frac{4}{\sqrt{114}}\right)^2-\frac{16}{114}-\frac{150}{19}=0
\]
より
\[
\left(\widetilde{x}-\frac{11}{2\sqrt{3}}\right)^2+ \left(\widetilde{y}-\frac{4}{\sqrt{114}}\right)^2=\frac{1377}{76} = \left(\frac{9\sqrt{17}}{2\sqrt{19}}\right)^2
\]
を得る.パラメータ $t$ を用いれば,この円は
\[
\widetilde{x}-\frac{11}{2\sqrt{3}} = \frac{9\sqrt{17}}{2\sqrt{19}}\cos{t}, \quad \widetilde{y}-\frac{4}{\sqrt{114}} = \frac{9\sqrt{17}}{2\sqrt{19}}\sin{t}
\]
と表示できるから,$\widetilde{z}$ 座標も考慮して
\[
\left[
\begin{array}{c}
\widetilde{x}(t) \\
\widetilde{y}(t) \\
\widetilde{z}(t)
\end{array}
\right]
=
\frac{1}{2\sqrt{57}}
\left[
\begin{array}{c}
11\sqrt{19} \\
4\sqrt{2} \\
10\sqrt{6}
\end{array}
\right]
+\frac{9\sqrt{17}}{2\sqrt{19}}
\left[
\begin{array}{c}
\cos{t}\\
\sin{t} \\
0
\end{array}
\right]
\]
と表現できる.
座標系を元に戻して中心,半径,パラメータ表示を求める
新しい座標系上で得られた円の表現を元の座標系で表現しなおせば
\[
\begin{align*}
\left[
\begin{array}{c}
x(t) \\
y(t) \\
z(t)
\end{array}
\right]
&=
A \left[
\begin{array}{c}
\widetilde{x}(t) \\
\widetilde{y}(t) \\
\widetilde{z}(t)
\end{array}
\right] \\
&=
\frac{1}{38}
\left[
\begin{array}{c}
121 \\
-39 \\
49
\end{array}
\right]
+
\frac{9\sqrt{17}}{2\sqrt{57}}
\left[
\begin{array}{c}
1 \\
-1 \\
1
\end{array}
\right]\cos{t}
+
\frac{9\sqrt{17}}{38\sqrt{6}}
\left[
\begin{array}{c}
1 \\
8 \\
7
\end{array}
\right]\sin{t} \\
&=
\frac{1}{38\sqrt{6}}\left[
\begin{array}{c}
\displaystyle 121\sqrt{6}+9\sqrt{17}\Bigl(\sqrt{38}\cos{t}+\sin{t}\Bigr) \\
\displaystyle -39\sqrt{6}-9\sqrt{17}\Bigl(\sqrt{38}\cos{t}-8\sin{t}\Bigr) \\
\displaystyle 49\sqrt{6}+9\sqrt{17}\Bigl(\sqrt{38}\cos{t}+7\sin{t}\Bigr)
\end{array}
\right]
\end{align*}
\]
を得る.これが求める円周のパラメータ表示である.パラメータ $t$ に依らない2行目の第1項目
\[
\frac{1}{38}
\left[
\begin{array}{c}
121 \\
-39 \\
49
\end{array}
\right]
\]
は(元の座標系での)円の中心の座標を表す.
