Stirling の公式
Stirling の近似公式の1つ
\[
\lim_{n \to \infty} \frac{n!}{\sqrt{2\pi n}(n/e)^n} = 1
\]
を Wallis 積分を利用して導出する方法についてまとめた.
目次
Stirling の公式
\[
\lim_{n \to \infty} \frac{n!}{\sqrt{2\pi n}(n/e)^n} = 1
\]
は $n$ が 十分に大きいとき,$n! \fallingdotseq \sqrt{2\pi n}(n/e)^n$ が成り立つことを意味する.これを以下のように $\sim$ 記号で表現する:
\[
n! \sim \sqrt{2\pi n}\left(\frac{n}{e}\right)^n
\]
この近似表現を Stirling の公式(Stirling の近似)という.
準備 1:
2つの数列 $\{a_n\} , \, \{b_n\}~~(n=1,2,\ldots)$ を
\[
a_n = \frac{n!}{\sqrt{n}n^ne^{-n}},\qquad b_n = \frac{4^{n}(n!)^2}{\sqrt{n}(2n)!}
\]
と定める.
補題 2:$b_n$ の極限
\[
\lim_{n \to \infty}b_n = \sqrt{\pi}
\]
詳細(click)
Wallis の公式の系より
\[
\lim_{n \to \infty}\frac{\sqrt{n}\cdot{}_{2n}{\rm C}_{n}}{4^n} = \frac{1}{\sqrt{\pi}}
\]
である.いま
\[
b_n = \frac{4^{n}(n!)^2}{\sqrt{n}(2n)!} = \frac{4^n}{\sqrt{n}\cdot{}_{2n}{\rm C}_{n}}
\]
であるから
\[
\lim_{n \to \infty}b_n = \sqrt{\pi}
\]
を得る.
補題 3:$\log{(1+x)}$ の評価
$0 < x < 1$ に対し
\[
x-\frac{x^2}{2} + \frac{x^3}{3}-\frac{x^4}{4} < \log{(1+x)} < x-\frac{x^2}{2} + \frac{x^3}{3}
\]
が成り立つ.
証明(click)
\[
f(x) = \log{(1+x)}-x + \frac{x^2}{2}-\frac{x^3}{3} + \frac{x^4}{4}
\]
とおく.
\[
f'(x) = \frac{1}{1+x}-\left(1-x + x^2-x^3\right) = \frac{1}{1+x}- \frac{1-x^4}{1+x} = \frac{x^4}{x+1} > 0
\]
であるから,$f(x)$ は $0 < x < 1$ で単調に増加する.ゆえに
\[
\log{(1+x)-x + \frac{x^2}{2}-\frac{x^3}{3} + \frac{x^4}{4}} = f(x) \geqq f(0) = 0
\]
を整理すれば求める不等式の左辺が評価できる.
\[
g(x) = \log{(1+x)}-x + \frac{x^2}{2}-\frac{x^3}{3}
\]
とおく.
\[
g'(x) = \frac{1}{1+x}-\left(1-x + x^2\right) = \frac{1}{1+x}-\frac{1+x^3}{1+x} =-\frac{x^3}{1+x} < 0
\]
であるから,$g(x)$ は $0 < x < 1$ で単調に減少する.ゆえに
\[
\log{(1+x)}-x + \frac{x^2}{2}-\frac{x^3}{3} = g(x) \leqq g(0) = 0
\]
を整理すれば求める不等式の右辺が評価できる.
補題 4:$\log{(a_{n}/a_{n+1})}$ の評価
$n = 2,3,\ldots$ に対して
\[
0 < \log{\frac{a_n}{a_{n+1}}} < \frac{1}{2n(n+1)}
\]
が成り立つ.
証明(click)
$$
\begin{eqnarray*}
\frac{a_n}{a_{n+1}} & = & \frac{n!}{\sqrt{n}n^ne^{-n}} \cdot \frac{\sqrt{n+1}(n+1)^{n+1}e^{-n-1}}{(n+1)!} \\
& = & \frac{n!}{\sqrt{n}n^ne^{-n}} \cdot \frac{\sqrt{n+1}(n+1)(n+1)^{n}e^{-n}e^{-1}}{(n+1)n!} \\
& = & \frac{\sqrt{n+1}}{\sqrt{n}}\cdot\frac{(n+1)^n}{n^n}\cdot e^{-1} \\
& = & \sqrt{\frac{n+1}{n}}\left(\frac{n+1}{n}\right)^n\cdot\frac{1}{e} \\
& = & \left(\frac{n+1}{n}\right)^{n+\frac{1}{2}}\cdot\frac{1}{e}
\end{eqnarray*}
$$
であるから
\[
\log{\frac{a_n}{a_{n+1}}} = \log{\left(\frac{n+1}{n}\right)^{n+\frac{1}{2}}\cdot\frac{1}{e}} = \left(n+\frac{1}{2}\right)\log{\left(1+\frac{1}{n}\right)}-1
\]
が成り立つ.いま,$n \geqq 2$ であるから $0 < 1/n < 1$ である.補題 3 において $x = 1/n$ とすれば
\[
\frac{1}{n}-\frac{1}{2n^2} + \frac{1}{3n^3}-\frac{1}{4n^4}< \log{\left(1+\frac{1}{n}\right)}< \frac{1}{n}-\frac{1}{2n^2} + \frac{1}{3n^3}
\]
\[
\frac{1}{12n^2}-\frac{1}{12n^3}-\frac{1}{8n^4} < \left(n + \frac{1}{2}\right)\log{\left(1 + \frac{1}{n}\right)} -1 < \frac{1}{12n^2} +\frac{1}{6n^3}
\]
\[
\frac{1}{12n^2}-\frac{1}{12n^3}-\frac{1}{8n^4} < \log{\frac{a_{n}}{a_{n+1}}}< \frac{1}{12n^2} +\frac{1}{6n^3}
\]
が成り立つ.不等式の最左辺については,$n \geqq 2$ のとき
\[
\frac{1}{12n^2}-\frac{1}{12n^3}-\frac{1}{8n^4} = \frac{2n^2-2n+3}{24n^4} > 0
\]
が成り立っている.最右辺については,$n > 1$ のとき
\[
\frac{2}{n(n+1)}-\frac{1}{n^2} = \frac{n-1}{n^2(n+1)} > 0
\]
より
\[
\frac{1}{n^2} < \frac{2}{n(n+1)}
\]
が成り立つことに注意すれば
\[
\frac{1}{12n^2} +\frac{1}{6n^3} < \frac{1}{12n^2} + \frac{1}{6n^2} = \frac{1}{4n^2} < \frac{1}{2n(n+1)}
\]
を得る.したがって
\[
0 < \log{\frac{a_n}{a_{n+1}}} < \frac{1}{2n(n+1)}
\]
が示された.
補題 5:$a_n/a_{2n}$ の極限
\[
\lim_{n \to \infty}\frac{a_{n}}{a_{2n}} = 1
\]
証明(click)
$$
\begin{eqnarray*}
\log{\frac{a_{n}}{a_{2n}}} & = & \log{\frac{a_{n}}{a_{n+1}}\cdot\frac{a_{n+1}}{a_{n+2}}\cdots\frac{a_{2n-2}}{a_{2n-1}}\cdot\frac{a_{2n-1}}{a_{2n}}} \\
& = & \log{\frac{a_{n}}{a_{n+1}}}+\log{\frac{a_{n+1}}{a_{n+2}}}+ \cdots + \log{\frac{a_{2n-2}}{a_{2n-1}}}+\log{\frac{a_{2n-1}}{a_{2n}}} \\
& = & \sum_{k=1}^{n}\log{\frac{a_{n+k-1}}{a_{n+k}}}
\end{eqnarray*}
$$
である.$\log{(a_{n}/a_{n+1})}$ の評価より
\[
0 < \sum_{k=1}^{n}\log{\frac{a_{n+k-1}}{a_{n+k}}} < \sum_{k=1}^{n}\frac{1}{2(n+k-1)(n+k)}
\]
であるが,最右辺については部分分数分解を用いて
$$
\begin{eqnarray*}
\sum_{k=1}^{n}\frac{1}{2(n+k-1)(n+k)} & = & \frac{1}{2}\sum_{k=1}^{n}\frac{1}{(n+k-1)(n+k)} \\
& = & \frac{1}{2}\sum_{k=1}^{n}\left(\frac{1}{n+k-1}-\frac{1}{n+k}\right) \\
& = & \frac{1}{2}\left\{\left(\frac{1}{n}-\frac{1}{n+1}\right) + \left(\frac{1}{n+1}-\frac{1}{n+2}\right) + \right. \\
& & \left. \cdots + \left(\frac{1}{n+n-1}-\frac{1}{n+n}\right)\right\} \\
& = & \frac{1}{2}\left(\frac{1}{n}-\frac{1}{2n}\right) \\
& = & \frac{1}{4n}
\end{eqnarray*}
$$
と計算できる.したがって
\[
0 < \log{\frac{a_{n}}{a_{2n}}} < \frac{1}{4n}
\]
が成り立つ.ここで $n \to \infty$ の極限をとれば,はさみうちの原理より
\[
\lim_{n \to \infty}\log{\frac{a_{n}}{a_{2n}}} = 0
\]
ゆえに
\[
\lim_{n \to \infty}\frac{a_{n}}{a_{2n}} = 1
\]
である.
定理 6:Stirling の公式
\[
\lim_{n \to \infty} \frac{n!}{\sqrt{2\pi n}(n/e)^n} = 1
\]
証明(click)
$$
\begin{eqnarray*}
a_n^2 & = & \frac{n!}{\sqrt{n} n^n e^{-n}} \cdot \frac{n!}{\sqrt{n} n^n e^{-n}}\\
& = & \frac{4^n(n!)^2}{\sqrt{n}(2n)!}\cdot\frac{(2n)!}{4^n \cdot \sqrt{2}\cdot \sqrt{n} n^{2n} e^{-2n}} \cdot \sqrt{2} \\
& = & \frac{4^n(n!)^2}{\sqrt{n}(2n)!}\cdot\frac{(2n)!}{\sqrt{2n}(2n)^{2n}e^{-2n}}\cdot \sqrt{2} \\
& = & b_n \cdot a_{2n} \cdot \sqrt{2}
\end{eqnarray*}
$$
であるから
\[
a_n = \sqrt{2}b_n \cdot \frac{a_{2n}}{a_{n}}
\]
が成り立つ.したがって $\{a_n\}$ の定義から
\[
\lim_{n \to \infty} \frac{n!}{\sqrt{2\pi n}(n/e)^n} = \lim_{n \to \infty} \frac{a_n}{\sqrt{2\pi}} = \lim_{n \to \infty}\frac{b_n}{\sqrt{\pi}} \cdot \frac{a_{2n}}{a_{n}} = 1 \cdot 1 = 1
\]
を得る.
補足
$a_n$ の図形的な意味
$k = 1 , 2 , \dots$ に対して,
- 曲線 $y = \log{x}$ 上の点 $\textrm{P}_k ~ (k , \log{k})$
- $x$ 軸上の点 $\textrm{Q}_k ~ (k , 0)$
を考える.$S_k$ を台形 $\textrm{P}_k\textrm{P}_{k+1}\textrm{Q}_{k+1}\textrm{Q}_k$ の面積とすると
\[
S_k = \frac{\log{k} + \log{(k+1)}}{2}
\]
が成り立つ.曲線 $y = \log{x}$ と直線 $x = n$ 及び $x$ 軸に囲まれた領域の面積を $A_n$ とすると
\[
A_n = \int_{1}^{n}\log{x}\,dx = n \log{n}-n + 1
\]
である.$n \geqq 2$ のとき,台形を足し合わせた
$$
\begin{align*}
T_n = \sum_{k=1}^{n-1}S_k
&= \frac{1}{2} \biggl((\log{1} + \log{2}) + (\log{2} + \log{3}) + \cdots + (\log{(n-1)} + \log{n})\biggr) \\
&= (\log{2} + \log{3} + \cdots + \log{(n-1)} + \log{n} )-\frac{1}{2}\log{n} \\
&= \log{n!}-\frac{1}{2}\log{n}
\end{align*}
$$
はグラフから $A_n > T_n$ を満たす.例えば下図の橙色の領域は $A_4-T_4$ である.
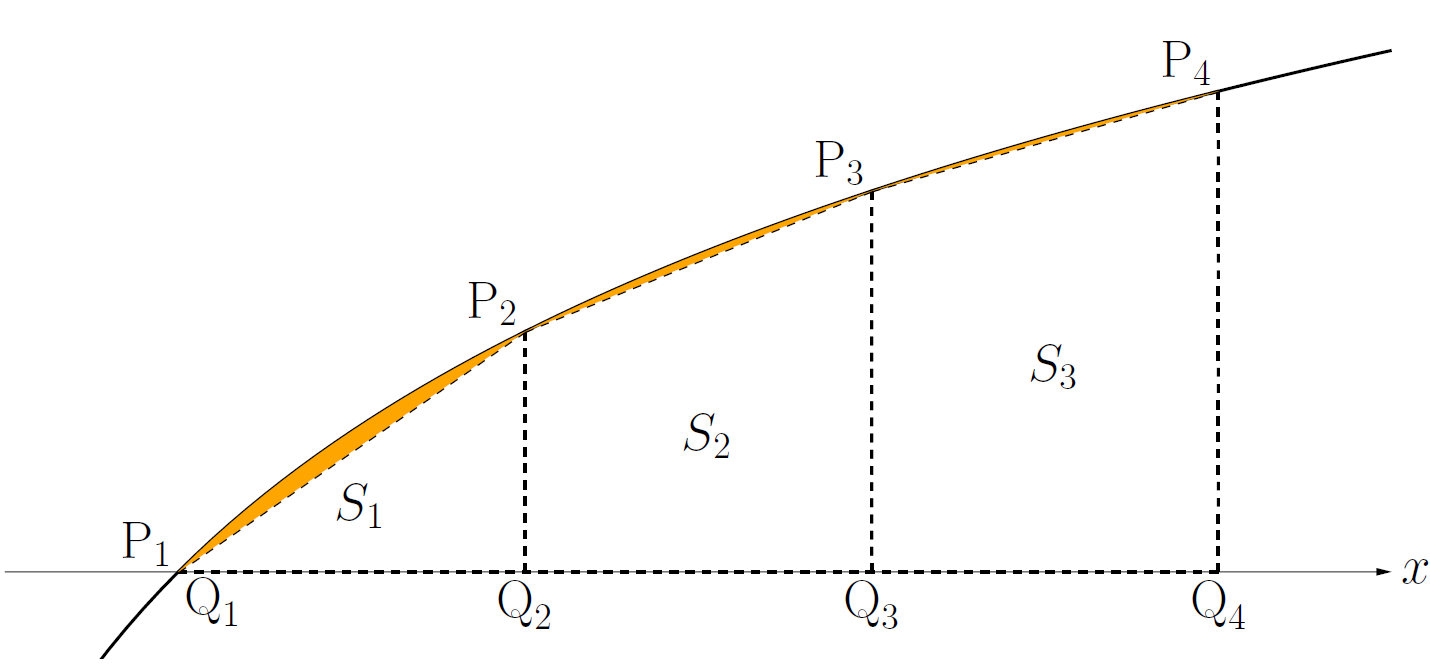
このとき
$$
\begin{align*}
A_n-T_n
&= \left(n + \frac{1}{2}\right)\log{n}-n + 1-\log{n!} \\
&= \log{\left(n^{n + 1/2}\right)}-\log{e^n} + 1-\log{n!} \\
&= \log{\frac{\sqrt{n}n^n}{n!e^n}} + 1 \\
&= 1-\log{a_n}
\end{align*}
$$
が成り立つ.したがって,$a_n$ はこのグラフの面積の差を表す指標とみなせる.
\[
\lim_{n \to \infty} \log{a_n} = \log{\sqrt{2\pi}} \fallingdotseq 0.9189 \cdots
\]
であるから,$A_n-T_n$ の極限は $0.081$ 程度の値となる.
20190602 更新
