三角形と位置ベクトル
空間内の三角形 $\triangle \textrm{ABC}$ の各頂点の位置ベクトルを用いて,三角形と同じ平面上にある任意の点 $\textrm{P}$ の位置ベクトルを表現することを考える.
記号のルール
- $\triangle \textrm{ABC}$ の面積を $S_{\triangle \textrm{ABC}}$ と表すことにする
三角形の内部の点の位置ベクトル
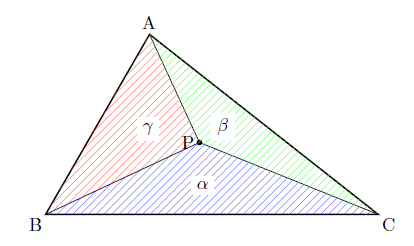
$\triangle \textrm{ABC}$ の内部の点 $\textrm{P}$ に対して
\[
S_{\triangle \textrm{PBC}} : S_{\triangle \textrm{PCA}} : S_{\triangle \textrm{PAB}} = \alpha : \beta : \gamma
\] であるとき
\[
\overrightarrow{\textrm{OP}} = \frac{\alpha \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{\alpha + \beta + \gamma}
\] が成り立つ.
証明(click)
直線 $\textrm{AP}$ と直線 $\textrm{BC}$ の交点を $\textrm{D}$ とする.
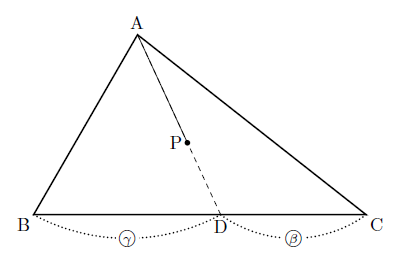
$S_{\triangle \textrm{ABC}} = (\alpha + \beta + \gamma)S$ とおくと
\[
\begin{align*}
S_{\triangle \textrm{PAB}}
&= S_{\triangle \textrm{ABC}} \times \frac{\gamma}{\alpha + \beta + \gamma} = \gamma S \\
S_{\triangle \textrm{PAC}}
&= S_{\triangle \textrm{ABC}} \times \frac{\beta}{\alpha + \beta + \gamma} = \beta S
\end{align*}
\] より
\[
\begin{align*}
S_{\triangle \textrm{ABD}}
&= S_{\triangle \textrm{PAB}} \times \frac{\textrm{AD}}{\textrm{AP}} = \gamma S \times \frac{\textrm{AD}}{\textrm{AP}} \\
S_{\triangle \textrm{ACD}}
&= S_{\triangle \textrm{PAC}} \times \frac{\textrm{AD}}{\textrm{AP}} = \beta S \times \frac{\textrm{AD}}{\textrm{AP}}
\end{align*}
\] であるから
\[
\textrm{BD} : \textrm{DC} = S_{\triangle \textrm{ABD}} : S_{\triangle \textrm{ACD}} = \gamma : \beta
\] が成り立つ.したがって
\[
\overrightarrow{\textrm{AD}} = \frac{\beta \overrightarrow{\textrm{AB}} + \gamma \overrightarrow{\textrm{AC}}}{\gamma + \beta}
\] である.また
\[
S_{\triangle \textrm{PBC}} = S_{\triangle \textrm{ABC}} \times \frac{\alpha}{\alpha + \beta + \gamma} = \alpha S
\] より
\[
S_{\triangle \textrm{ABC}} : S_{\triangle \textrm{PBC}} = \alpha + \beta + \gamma : \alpha
\] が成り立つので
\[
\textrm{AD} : \textrm{PD} = \alpha + \beta + \gamma : \alpha
\] より
\[
\textrm{AD} : \textrm{AP} = \alpha + \beta + \gamma : \beta + \gamma
\] が成り立つ.したがって
\[
\overrightarrow{\textrm{AP}} = \frac{\beta + \gamma}{\alpha + \beta + \gamma}\overrightarrow{\textrm{AD}} = \frac{\beta \overrightarrow{\textrm{AB}} + \gamma \overrightarrow{\textrm{AC}}}{\alpha + \beta + \gamma}
\] を得る.それぞれのベクトルを $\overrightarrow{\textrm{OP}}$,$\overrightarrow{\textrm{OA}}$,$\overrightarrow{\textrm{OB}}$,$\overrightarrow{\textrm{OC}}$ で表すと
\[
\overrightarrow{\textrm{OP}}-\overrightarrow{\textrm{OA}} = \frac{\beta (\overrightarrow{\textrm{OB}}-\overrightarrow{\textrm{OA}}) + \gamma (\overrightarrow{\textrm{OC}}-\overrightarrow{\textrm{OA}})}{\alpha + \beta + \gamma}
\] であるから,これを整理して
\[
\overrightarrow{\textrm{OP}} = \frac{\alpha \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{\alpha + \beta + \gamma}
\] を得る.
三角形の外部の点の位置ベクトル
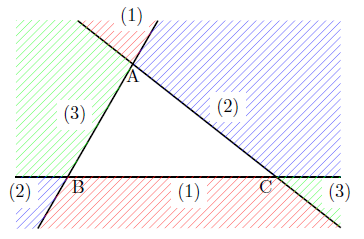
$\triangle \textrm{ABC}$ の外部の点 $\textrm{P}$ に対して
\[
S_{\triangle \textrm{PBC}} : S_{\triangle \textrm{PCA}} : S_{\triangle \textrm{PAB}} = \alpha : \beta : \gamma
\] であるとき
\[
\overrightarrow{\textrm{OP}} =
\begin{cases}
\displaystyle \frac{-\alpha \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{-\alpha + \beta + \gamma} & \text{(点 $\textrm{P}$ が領域 (1) にあるとき)} \\ \\
\displaystyle \frac{+ \alpha \overrightarrow{\textrm{OA}}-\beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{+ \alpha-\beta + \gamma} & \text{(点 $\textrm{P}$ が領域 (2) にあるとき)} \\ \\
\displaystyle \frac{+ \alpha \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}}-\gamma \overrightarrow{\textrm{OC}}}{+ \alpha + \beta-\gamma} & \text{(点 $\textrm{P}$ が領域 (3) にあるとき)}
\end{cases}
\] が成り立つ.
証明(click)
点 $\textrm{P}$ が領域 (1) にある場合について
- 頂点 $\textrm{A}$ からみて,点 $\textrm{P}$ が辺 $\textrm{BC}$ と逆側にあるとき
- 頂点 $\textrm{A}$ からみて,点 $\textrm{P}$ が辺 $\textrm{BC}$ の向こう側にあるとき
に分けて示す.また
\[
S_{\triangle \textrm{PBC}} : S_{\triangle \textrm{PCA}} : S_{\triangle \textrm{PAB}} = \alpha : \beta : \gamma
\]より
\[
S_{\triangle \textrm{PBC}} = \alpha S, \quad S_{\triangle \textrm{PCA}} = \beta S, \quad S_{\triangle \textrm{PAB}} = \gamma S
\]を満たす正の数 $S$ が存在することに注意する.
まず,頂点 $\textrm{A}$ からみて,点 $\textrm{P}$ が辺 $\textrm{BC}$ と逆側にあるときを示す.このとき点 $\textrm{A}$ は $\triangle \textrm{PBC}$ の内部の点と考えることができる.
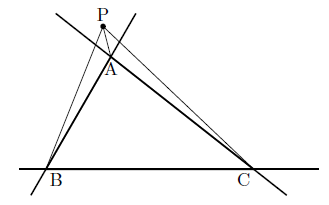
いま
\[
\begin{align*}
S_{\triangle \textrm{APB}}
&= \gamma S \\
S_{\triangle \textrm{APC}}
&= \beta S \\
S_{\triangle \textrm{ABC}}
&= S_{\triangle \textrm{PBC}}-S_{\triangle \textrm{APB}}-S_{\triangle \textrm{APC}} = \alpha S-\gamma S-\beta S
\end{align*}
\] であるから
\[
S_{\triangle \textrm{ABC}} : S_{\triangle \textrm{APC}} : S_{\triangle \textrm{APB}} = \alpha-\beta-\gamma : \beta : \gamma
\] が成り立つ.ゆえに三角形の内部の点の位置ベクトルの式より
\[
\overrightarrow{\textrm{OA}} = \frac{(\alpha-\beta-\gamma)\overrightarrow{\textrm{OP}} + \beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{(\alpha-\beta-\gamma) + \beta + \gamma} = \frac{(\alpha-\beta-\gamma)\overrightarrow{\textrm{OP}} + \beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{\alpha}
\] である.これを $\overrightarrow{\textrm{OP}}$ について整理すれば
\[
\overrightarrow{\textrm{OP}} = \frac{-\alpha \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{-\alpha + \beta + \gamma}
\] が得られる.
次に,頂点 $\textrm{A}$ からみて,点 $\textrm{P}$ が辺 $\textrm{BC}$ の向こう側にあるときを示す.このとき半直線 $\textrm{AB}$ 上に $\textrm{AB} : \textrm{AB}’ = 1 : n$ となるような点 $\textrm{B}’$ を,半直線 $\textrm{AC}$ 上に $\textrm{AC} : \textrm{AC}’ = 1 : n$ となるような点 $\textrm{C}’$ をとって,点 $\textrm{P}$ が $\triangle \textrm{A}\textrm{B}’\textrm{C}’$ の内部の点になるようにすることができる.
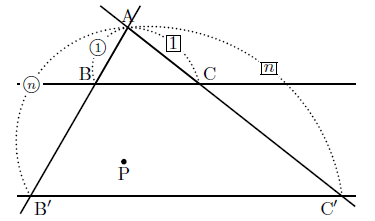
いま
\[
\begin{align*}
S_{\triangle \textrm{P}\textrm{A}\textrm{B}’}
&= n S_{\triangle \textrm{PAB}} = n \gamma S \\
S_{\triangle \textrm{P}\textrm{A}\textrm{C}’}
&= n S_{\triangle \textrm{PAC}} = n \beta S
\end{align*}
\] であり,また
\[
\begin{align*}
S_{\triangle \textrm{A}\textrm{B}\textrm{C}}
&= S_{\triangle \textrm{P}\textrm{A}\textrm{B}} + S_{\triangle \textrm{P}\textrm{A}\textrm{C}}-S_{\triangle \textrm{P}\textrm{B}\textrm{C}} \\
&= \gamma S + \beta S-\alpha S \\
&= (\beta + \gamma-\alpha)S
\end{align*}
\] であるから
\[
\begin{align*}
S_{\triangle \textrm{P}\textrm{B}’\textrm{C}’}
&= S_{\triangle \textrm{A}\textrm{B}’\textrm{C}’}-S_{\triangle \textrm{P}\textrm{A}\textrm{B}’}-S_{\triangle \textrm{P}\textrm{A}\textrm{C}’} \\
&= n^2 S_{\triangle \textrm{A}\textrm{B}\textrm{C}}-n \gamma S-n \beta S \\
&= n^2 (\beta + \gamma-\alpha)S-n \gamma S-n \beta S
\end{align*}
\] が成り立つ.したがって
\[
\begin{align*}
S_{\triangle \textrm{P}\textrm{B}’\textrm{C}’} : S_{\triangle \textrm{P}\textrm{C}’\textrm{A}} : S_{\triangle \textrm{P}\textrm{A}\textrm{B}’}
&= n^2 (\beta + \gamma-\alpha) S-n \gamma S-n \beta S : n \beta S : n \gamma S \\
&= n (\beta + \gamma-\alpha)-\gamma-\beta : \beta : \gamma
\end{align*}
\] であるから,三角形の内部の点の位置ベクトルの式より
\[
\begin{align*}
\overrightarrow{\textrm{OP}}
&= \frac{(n \beta + n \gamma-n \alpha-\beta-\gamma) \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}’} + \gamma \overrightarrow{\textrm{OC}’}}{ (n \beta + n \gamma-n \alpha-\gamma-\beta) + \beta + \gamma} \\
&= \frac{(n \beta + n \gamma-n \alpha-\beta-\gamma) \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}’} + \gamma \overrightarrow{\textrm{OC}’}}{n (\beta + \gamma-\alpha)}
\end{align*}
\] が成り立つ.ここで
\[
\begin{align*}
\overrightarrow{\textrm{OB}’}
&= \overrightarrow{\textrm{OA}} + \overrightarrow{\textrm{AB}’} \\
&= \overrightarrow{\textrm{OA}} + n \overrightarrow{\textrm{AB}} \\
&= \overrightarrow{\textrm{OA}} + n (\overrightarrow{\textrm{OB}}-\overrightarrow{\textrm{OA}}) \\
&= (1-n) \overrightarrow{\textrm{OA}} + n \overrightarrow{\textrm{OB}} \\
\overrightarrow{\textrm{OC}’}
&= \overrightarrow{\textrm{OA}} + \overrightarrow{\textrm{AC}’} \\
&= \overrightarrow{\textrm{OA}} + n \overrightarrow{\textrm{AC}} \\
&= \overrightarrow{\textrm{OA}} + n (\overrightarrow{\textrm{OC}}-\overrightarrow{\textrm{OA}}) \\
&= (1-n) \overrightarrow{\textrm{OA}} + n \overrightarrow{\textrm{OC}}
\end{align*}
\] であるから
\[
\begin{align*}
\overrightarrow{\textrm{OP}}
&= \frac{(n \beta + n \gamma-n \alpha-\beta-\gamma) \overrightarrow{\textrm{OA}} + (1-n) \beta \overrightarrow{\textrm{OA}} + n \beta \overrightarrow{\textrm{OB}} + (1-n) \gamma \overrightarrow{\textrm{OA}} + n \gamma \overrightarrow{\textrm{OC}}}{n (\beta + \gamma-\alpha)} \\
&= \frac{-\alpha \overrightarrow{\textrm{OA}} + \beta \overrightarrow{\textrm{OB}} + \gamma \overrightarrow{\textrm{OC}}}{-\alpha + \beta + \gamma}
\end{align*}
\] が得られる.