三角形の重心・外心・内心・垂心の位置ベクトル
空間内の三角形 $\triangle \textrm{ABC}$ の各頂点の位置ベクトルを用いて,三角形の重心,外心,内心,垂心の位置ベクトルを表現することを考える.
導出には以下のノートの結果を利用する:
記号のルール
- $\triangle \textrm{ABC}$ の面積を $S_{\triangle \textrm{ABC}}$ と表すことにする
- $\angle \textrm{CAB} = A$,$\angle \textrm{ABC} = B$,$\angle \textrm{BCA} = C$ と表現する
- $\textrm{BC} = a$,$\textrm{CA} = b$,$\textrm{AB} = c$ と表現する
重心の位置ベクトル
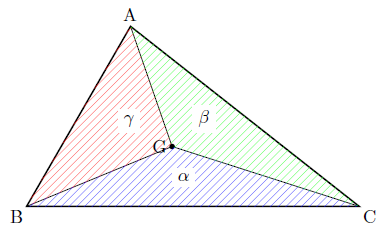
$\triangle \textrm{ABC}$ および重心 $\textrm{G}$ に対して
\[
\overrightarrow{\textrm{OG}} = \frac{\overrightarrow{\textrm{OA}} + \overrightarrow{\textrm{OB}} + \overrightarrow{\textrm{OC}}}{3}
\] が成り立つ.
証明(click)
直線 $\textrm{AG}$ と直線 $\textrm{BC}$ の交点を $\textrm{D}$ とする.
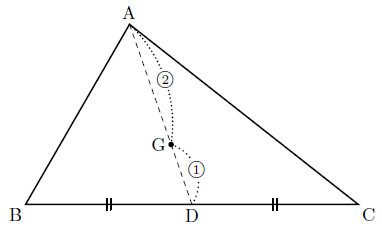
重心の性質より $\textrm{AG} : \textrm{GD} = 2 : 1$ であるから
\[
S_{\triangle \textrm{GBC}} = \frac{1}{3} S_{\triangle \textrm{ABC}}
\] である.$S_{\triangle \textrm{GCA}}$ および $S_{\triangle \textrm{GAB}}$ も同様であるから
\[
\alpha : \beta : \gamma = S_{\triangle \textrm{GBC}} : S_{\triangle \textrm{GCA}} : S_{\triangle \textrm{GAB}} = 1: 1: 1
\] を得る.したがって
\[
\overrightarrow{\textrm{OG}} = \frac{\overrightarrow{\textrm{OA}} + \overrightarrow{\textrm{OB}} + \overrightarrow{\textrm{OC}}}{3}
\] である.
外心の位置ベクトル
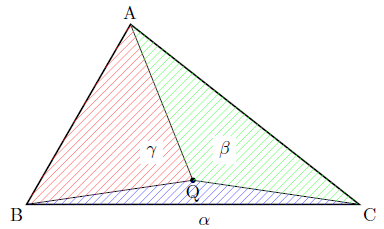
$\triangle \textrm{ABC}$ および外心 $\textrm{Q}$ に対して
\[
\overrightarrow{\textrm{OQ}} = \frac{(\sin{2A}) \overrightarrow{\textrm{OA}} + (\sin{2B}) \overrightarrow{\textrm{OB}} + (\sin{2C}) \overrightarrow{\textrm{OC}}}{\sin{2A} + \sin{2B} + \sin{2C}}
\] が成り立つ.
鋭角三角形の場合の証明(click)
$\triangle \textrm{ABC}$ が鋭角三角形の場合,すなわち外心 $\textrm{Q}$ が $\triangle \textrm{ABC}$ の内部にある場合を考える.外接円の半径を $R$ とおく.
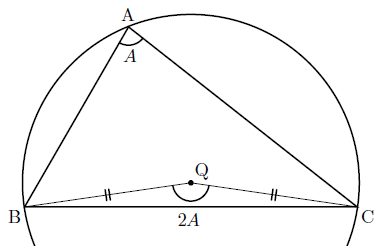
外心の性質より $\textrm{QB} = \textrm{QC} = R$ である.また,円周角の定理より $\angle \textrm{BQC} = 2A$ である.したがって
\[
S_{\triangle \textrm{QBC}} = \frac{1}{2} \cdot R^2 \cdot \sin{2A}
\] が成り立つ.同様にして
\[
S_{\triangle \textrm{QCA}} = \frac{1}{2} \cdot R^2 \cdot \sin{2B}, \quad S_{\triangle \textrm{QAB}} = \frac{1}{2} \cdot R^2 \cdot \sin{2C}
\] が成り立つから
\[
\alpha : \beta : \gamma = S_{\triangle \textrm{QBC}} : S_{\triangle \textrm{QCA}} : S_{\triangle \textrm{QAB}} = \sin{2A} : \sin{2B} : \sin{2C}
\] を得る.したがって
\[
\overrightarrow{\textrm{OQ}} = \frac{(\sin{2A}) \overrightarrow{\textrm{OA}} + (\sin{2B}) \overrightarrow{\textrm{OB}} + (\sin{2C}) \overrightarrow{\textrm{OC}}}{\sin{2A} + \sin{2B} + \sin{2C}}
\] である.
鈍角三角形の場合の証明(click)
$\triangle \textrm{ABC}$ が鈍角三角形の場合,すなわち外心 $\textrm{Q}$ が $\triangle \textrm{ABC}$ の外部にある場合を考える.$\triangle \textrm{ABC}$ の外接円と直線 $\textrm{AQ}$ の交点のうち,点 $\textrm{A}$ でないものを $\textrm{A}’$ とする.
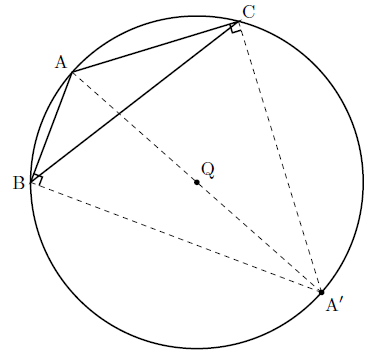
円に内接する四角形の性質より $\angle BA’C = \pi-A$ であるから
\[
\sin{(2 \angle BA’C)} = \sin{(2\pi-2A)} =-\sin{2A}
\] が成り立つ.また $\angle ABA’ = \angle ACA’ = \pi/2$ より
\[
\sin{(2 \angle CBA’)} = \sin{(\pi-2B)} = \sin{2B}, \quad \sin{(2 \angle BCA’)} = \sin{(\pi-2C)} = \sin{2C}
\] が成り立つから,$\triangle \textrm{A}’\textrm{B}\textrm{C}$ とその内部の外心 $\textrm{Q}$ に対する位置ベクトルは
\[
\begin{align*}
\overrightarrow{\textrm{OQ}}
&= \frac{(\sin{(2 \angle BA’C)}) \overrightarrow{\textrm{OA}} + (\sin{(2 \angle CBA’)}) \overrightarrow{\textrm{OB}} + (\sin{(2 \angle BCA’)}) \overrightarrow{\textrm{OC}}}{\sin{(2 \angle BA’C)} + \sin{(2 \angle CBA’)} + \sin{(2 \angle BCA’)}} \\
&= \frac{(-\sin{2A}) \overrightarrow{\textrm{OA}} + (\sin{2B}) \overrightarrow{\textrm{OB}} + (\sin{2C}) \overrightarrow{\textrm{OC}}}{-\sin{2A} + \sin{2B} + \sin{2C}}
\end{align*}
\] を満たす.ここで
\[
\overrightarrow{\textrm{OA$’$}} = \overrightarrow{\textrm{OA}} + 2 \overrightarrow{\textrm{AQ}} = \overrightarrow{\textrm{OA}} + 2 \overrightarrow{\textrm{OQ}}-2 \overrightarrow{\textrm{OA}} =-\overrightarrow{\textrm{OA}} + 2 \overrightarrow{\textrm{OQ}}
\] であるから,これを用いて整理すると
\[
\overrightarrow{\textrm{OQ}} = \frac{(\sin{2A}) \overrightarrow{\textrm{OA}} + (\sin{2B}) \overrightarrow{\textrm{OB}} + (\sin{2C}) \overrightarrow{\textrm{OC}}}{\sin{2A} + \sin{2B} + \sin{2C}}
\] が得られる.
内心の位置ベクトル
$\triangle \textrm{ABC}$ および内心 $\textrm{I}$ に対して
\[
\overrightarrow{\textrm{OI}} = \frac{a \overrightarrow{\textrm{OA}} + b \overrightarrow{\textrm{OB}} + c \overrightarrow{\textrm{OC}}}{a + b + c}
\] が成り立つ.
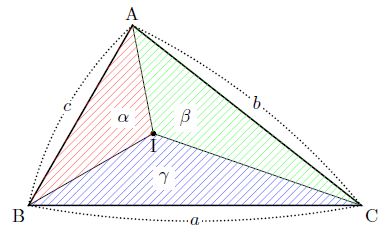
証明(click)
内接円の半径を $r$ とおく.
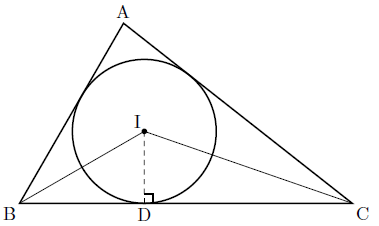
内心の性質より,点 $\textrm{I}$ から各辺に下した垂線の長さは $r$ であるから
\[
S_{\triangle \textrm{IBC}} = \frac{1}{2} ar
\] が成り立つ.同様にして
\[
S_{\triangle \textrm{ICA}} = \frac{1}{2} br, \quad S_{\triangle \textrm{IAB}} = \frac{1}{2} cr
\] が成り立つから
\[
\alpha : \beta : \gamma = S_{\triangle \textrm{IBC}} : S_{\triangle \textrm{ICA}} : S_{\triangle \textrm{IAB}} = a : b : c
\] を得る.したがって
\[
\overrightarrow{\textrm{OI}} = \frac{a \overrightarrow{\textrm{OA}} + b \overrightarrow{\textrm{OB}} + c \overrightarrow{\textrm{OC}}}{a + b + c}
\] である.
垂心の位置ベクトル
$\triangle \textrm{ABC}$ および垂心 $\textrm{H}$ に対して
\[
\overrightarrow{\textrm{OH}} = \frac{(\tan{A}) \overrightarrow{\textrm{OA}} + (\tan{B}) \overrightarrow{\textrm{OB}} + (\tan{C}) \overrightarrow{\textrm{OC}}}{\tan{A} + \tan{B} + \tan{C}}
\] が成り立つ.
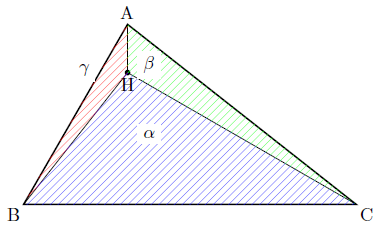
鋭角三角形の場合の証明(click)
$\triangle \textrm{ABC}$ が鋭角三角形の場合,すなわち垂心 $\textrm{H}$ が $\triangle \textrm{ABC}$ の内部にある場合を考える.直線 $\textrm{AH}$ と直線 $\textrm{BC}$ の交点を $\textrm{D}$ とする.
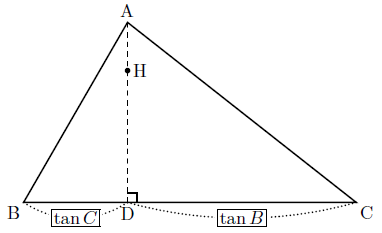
垂心の性質より $\triangle \textrm{ABD}$ および $\triangle \textrm{ACD}$ は直角三角形であるから
\[
\tan{B} = \frac{\textrm{AD}}{\textrm{BD}}, \quad \tan{C} = \frac{\textrm{AD}}{\textrm{DC}}
\] である.したがって
\[
\textrm{BD} : \textrm{DC} = \frac{\textrm{AD}}{\tan{B}} : \frac{\textrm{AD}}{\tan{C}} = \tan{C} : \tan{B}
\] が成り立つから
\[
S_{\triangle \textrm{HAB}} : S_{\triangle \textrm{HCA}} = \frac{1}{2} \cdot \textrm{AH} \cdot \textrm{BD} : \frac{1}{2} \cdot \textrm{AH} \cdot \textrm{DC} = \textrm{BD} : \textrm{DC} = \tan{C} : \tan{B}
\] である.同様にして $S_{\triangle \textrm{HBC}}$ について考えれば
\[
\alpha : \beta : \gamma = S_{\triangle \textrm{HBC}} : S_{\triangle \textrm{HCA}} : S_{\triangle \textrm{HAB}} = \tan{A}: \tan{B}: \tan{C}
\] を得る.したがって
\[
\overrightarrow{\textrm{OH}} = \frac{(\tan{A}) \overrightarrow{\textrm{OA}} + (\tan{B}) \overrightarrow{\textrm{OB}} + (\tan{C}) \overrightarrow{\textrm{OC}}}{\tan{A} + \tan{B} + \tan{C}}
\] である.
鈍角三角形の場合の証明(click)
$\triangle \textrm{ABC}$ が鈍角三角形の場合,すなわち垂心 $\textrm{H}$ が $\triangle \textrm{ABC}$ の外部にある場合を考える.ここで,$A + B + C = \pi$ であるから,正接の加法定理より
\[
\tan{A} = \tan{(\pi-(B + C))} =-\tan{(B+C)} = \frac{\tan{B} + \tan{C}}{\tan{B} \tan{C}-1}
\] が成り立つので
\[
\tan{A} \tan{B} \tan{C} = \tan{A} + \tan{B} + \tan{C}
\] であることに注意する.いま,垂心の性質から点 $\textrm{A}$ は鋭角三角形 $\triangle \textrm{HBC}$ の垂心である.
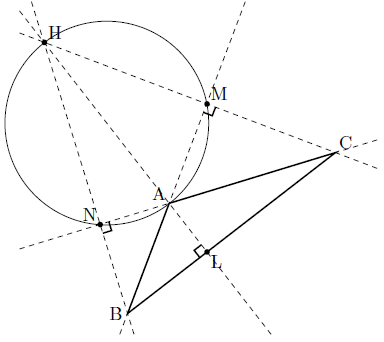
\[
\tan{(\angle \textrm{HBC})} = \tan{\left(\frac{\pi}{2}-C\right)} = \frac{1}{\tan{C}}, \quad \tan{(\angle \textrm{HCB})} = \tan{\left(\frac{\pi}{2}-B\right)} = \frac{1}{\tan{B}},
\] である.また,直線 $\textrm{HB}$ と直線 $\textrm{CA}$ の 交点を $\textrm{N}$,直線 $\textrm{HC}$ と直線 $\textrm{BA}$ の 交点を $\textrm{M}$ とすると,四角形 $\textrm{AMHN}$ が同一円周上にあることから
\[
\tan{(\angle \textrm{BHC})} = \tan{(\pi-\angle \textrm{NAM})} =-\tan{(\angle \textrm{NAM})} =-\tan{A}
\] が成り立つので,$\triangle \textrm{HBC}$ とその内部の垂心 $\textrm{A}$ の位置ベクトルは
\[
\begin{align*}
\overrightarrow{\textrm{OA}}
&= \frac{(-\tan{A}) \overrightarrow{\textrm{OA}} + \left(\frac{1}{\tan{C}}\right) \overrightarrow{\textrm{OB}} + \left(\frac{1}{\tan{B}}\right) \overrightarrow{\textrm{OC}}}{-\tan{A} + \frac{1}{\tan{C}} + \frac{1}{\tan{B}}} \\
&= \frac{(-\tan{A}\tan{B}\tan{C}) \overrightarrow{\textrm{OA}} + (\tan{B}) \overrightarrow{\textrm{OB}} + (\tan{C}) \overrightarrow{\textrm{OC}}}{-\tan{A}\tan{B}\tan{C} + \tan{B} + \tan{C}} \\
&= \frac{(-\tan{A}-\tan{B}-\tan{C}) \overrightarrow{\textrm{OA}} + (\tan{B}) \overrightarrow{\textrm{OB}} + (\tan{C}) \overrightarrow{\textrm{OC}}}{-\tan{A}}
\end{align*}
\] これを $\overrightarrow{\textrm{OH}}$ について整理すれば
\[
\overrightarrow{\textrm{OH}} = \frac{(\tan{A}) \overrightarrow{\textrm{OA}} + (\tan{B}) \overrightarrow{\textrm{OB}} + (\tan{C}) \overrightarrow{\textrm{OC}}}{\tan{A} + \tan{B} + \tan{C}}
\] を得る.
直角三角形の場合の補足(click)
直角三角形のとき,垂心は直角の頂点と一致する.例えば $\angle A = \pi/2$ のとき,垂心は点 $\textrm{A}$ と一致するが,このとき $\tan{A}$ は定義されない.一方,$\tan{\theta} = \sin{\theta}/\cos{\theta}$ を利用して
\[
\overrightarrow{\textrm{OH}} = \frac{(\sin{A} \cos{B} \cos{C}) \overrightarrow{\textrm{OA}} + (\sin{B} \cos{C} \cos{A}) \overrightarrow{\textrm{OB}} + (\sin{C} \cos{A} \cos{B}) \overrightarrow{\textrm{OC}}}{\sin{A} \cos{B} \cos{C} + \sin{B} \cos{C} \cos{A} + \sin{C} \cos{A} \cos{B}}
\] と表現すれば,$\sin{(\pi/2)} = 1$,$\cos{(\pi/2)} = 0$ であるから
\[
\overrightarrow{\textrm{OH}} = \frac{(\cos{B} \cos{C}) \overrightarrow{\textrm{OA}}}{\cos{B} \cos{C}} = \overrightarrow{\textrm{OA}}
\] となる.したがって,この式は直角三角形の場合も成立していると考えることができる.